Computer Vision, Chapter 1: Digital Topology Copyright © by V. Miszalok, last update: 2011-03-11
Let me know what you think	Digitale Geometrie   Problem der 8er-Nachbarschaft   Raster = Zellenkomplex aus 3D-, 2D-, 1D und 0D- Zellen   Der alte Kettencode = Freeman Code: falsch aber populär

Digitale Geometrie

In der klassischen Geometrie hat ein Punkt in der Ebene unendlich viele Nachbarn, aber so eine Ebene kann ein Computer nicht abbilden. Im Computer hat jeder Punkt der Ebene nicht unendlich viele, sondern nur 4 oder 8, jedenfalls eine finite Anzahl von Nachbarn wie eine Kachel an der Wand. Die Rastermatrix beschreibt eine lokal finite Ebene, wo andere Gesetze für Distanz, Fläche, Zusammenhang, Begrenzung gelten als in der 2000 Jahre alten, uns vertrauten analytischen Geometrie. Der Siegeszug der Rastergraphik erzwingt die Erfindung und Verwendung dieser neuen Denkweise, die man digitale Geometrie oder digitale Topologie nennt (von griechisch topos = der Raum). Ohne diese Denkweise fehlt die professionelle Grundlage für moderne Rastergraphiksoftware.

Pionier und Doyen der "digitalen Geometrie" und deren weltweite Autorität ist Prof. Dr. Wladimir Kovalevski, langjähriger Professor am FB Informatik der TFH Berlin. Siehe: www.kovalevsky.de/PublicationsE.htm Recent summary of Kovalevski's algorithms (preliminary) see: ../kovalevski.pdf (248 KB) Kovalevski untersucht die neuen Probleme des Zusammenhangs und der Begrenzung von Rastergebieten. Er beschreibt die neue Denkweise und erarbeitet die Axiomatik des lokal finiten Raums. Mit Hilfe der Zell-Topologie = Cellular Topology entwickelt er die Basisalgorithmen der Rastergraphik. Warnung: Ohne die Grundkenntnisse der "digitalen Geometrie" kann man keine guten und eleganten Rastergraphik-Programme schreiben.

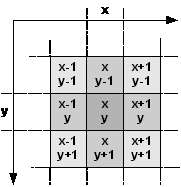Falls es nicht am Bildrand liegt, hat jedes Pixel x,y vier Nachbarn erster Klasse und vier Nachbarn zweiter Klasse. Mit den ersteren hat es eine Kante = Gartenzaun gemeinsam, mit den letzteren nur einen Punkt = Eckpfahl. Die Nachbarn der ersten Klasse nennt man die 4er Nachbarn, alle Nachbarn beider Klassen nennt man die 8er Nachbarn. Zweifellos kann Pixel x,y den Gartenzaun zu einem seiner 4er Nachbarn niederreißen und mit dessen Grundstück ein Gebiet bilden. Das ist aber schwieriger mit einem Nachbarn zweiter Klasse. Kann man den Eckpfahl niederreißen und wenn ja, was hat man davon ? Grundlegend: Die Elemente eines 2D-Rasters darf man sich keineswegs punktförmig denken, sondern als Rechteckflächen, vergleichbar mit rechtwinkligen Grundstücken oder Kacheln eines Badezimmers oder Feldern eines Schachbretts.

Problem der 8er-Nachbarschaft

In Bild1 herrscht 4er Nachbarschaft mit klaren Verhältnissen. Bild2 suggeriert, dass die 4 Einsen über Eck ebenfalls zusammenhängen, was bedeutet, die Anschauung akzeptiert die 8er Nachbarschaft genauso wie die 4er Nachbarschaft. Wir empfinden die 4 Einsen als ein schräges Gebiet der Fläche 4, welche zwei Hintergrundgebiete voller Nullen voneinander trennt, ohne dass wir den Widerspruch bemerken. Der Widerspruch liegt in der mangelnden Symmetrie zwischen Einsen und Nullen. Wenn die Einsen über Eck zusammenhängen, dürfen die Nullen keinesfalls auch über Eck zusammenhängen, sonst würde der Hintergrund den Vordergrund durchdringen was gegen jede Logik verstieße.
Es gibt zwei Möglichkeiten, den Widerspruch aus der Welt zu schaffen:
1) Man akzeptiert grundsätzlich keinerlei 8er Nachbarschaft, obwohl die Intuition diese suggeriert.
D.h. man verlangt, dass Vordergrundgebiete in 4er-Nachbarschaft zusammenhängen müssen wie in Bild4.
Vorteil: Mathematisch korrekt und widerspruchsfrei und Symmetrie zwischen Vorder- und Hintergrund.
Nachteil: Alle schrägen Linien müssen doppelt dick sein wie in Bild4.
2) Man akzeptiert 8er Nachbarschaft als von der Natur gegeben, aber nur im Vordergrund. Im Hintergrund gilt gleichzeitig immer nur 4er Nachbarschaft.
Vorteil: Entspricht der Anschauung.
Nachteil: Asymmetrie: Einsen und Nullen sind nicht gleichberechtigt. Das bedeutet, dass Vorder-Hintergrundsvertauschungen wie in Bild3 ins logische Chaos führen und deshalb verboten werden müssen.

Raster = Zellenkomplex aus 3D-, 2D-, 1D und 0D- Zellen

8er-Nachbarn haben mindestens einen gemeinsamen Punkt = Grundstücksecke, während 4er Nachbarn 2 gemeinsame Punkte und eine gemeinsame Kante = Grundstückszaun haben.
Die Begriffe "Kante" und "Eckpunkt" werden erweitert, systematisiert und präziser gefasst durch den Begriff "Zellen":
Dabei muss man Abschied nehmen von der naiven Auffassung, ein Raster sei eine Versammlung gleichartiger und gleichberechtigter Elemente = Pixel oder Voxel.
Ein Raster (= Zellenkomplex) ist in Wahrheit aufgebaut durch 4 verschiedene Typen von Zellen:
- 3-dimensionale (= volumenhafte) Zellen = 3D-Cells = Würfel oder Voxel
- 2-dimensionale (= flächenhafte) Zellen = 2D-Cells = Kacheln oder Pixel
- 1-dimensionale (= linienhafte ) Zellen = 1D-Cells = Fugen ( engl. cracks )
- 0-dimensionale (= punkthafte  ) Zellen = 0D-Cells = Eckpunkte ( engl. points )

Berandungsrelation: Eine Zelle wird ausschließlich berandet von Zellen niederer Dimensionen.
Voxel werden nicht von ihren Nachbarvoxeln berandet, sondern von Pixeln, Cracks und Points.
Pixel werden nicht von ihren Nachbarpixeln berandet, sondern von Cracks und Points.
Cracks werden nicht von ihren Nachbarcracks berandet sondern von Points.
Beispiele:
Ein einzelnes Voxel wird berandet von 6 Pixeln, 12 Cracks, 8 Points.
Ein einzelnes Pixel wird berandet von 4 Cracks, 4 Points.
Ein einzelner Crack wird berandet von 2 Points.
Wir beschränken uns im folgenden auf 2D-Raster mit den Zelltypen Pixel, Cracks und Points, obwohl alle Aussagen sinngemäß auch für Voxelgraphiken gelten.
Wichtig: Eine Rastergraphik besteht keineswegs nur aus einer Anhäufung gleichartiger Elemente (etwa Pixel). Sie muß betrachtet werden als eine Hierarchie von Elementen, die sich entweder beranden oder nicht.
Wichtige Folge: Man kann die Begrenzungen zwischen Pixeln nicht zusammen mit den Pixeln in einer einzigen Matrix codieren. Man braucht dazu 3 weitere Matrizen:
1. Die Matrix der vertikalen Cracks
2. Die Matrix der horizontalen Cracks
3. Die Matrix der Points
Diese drei weiteren Matrizen müssen nicht unbedingt physikalisch im Speicher vorhanden sein, sie müssen aber "mitgedacht" werden.

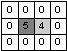0 bedeutet schwarz 5 bedeutet eine hohe und 4 eine etwas niedrigere Helligkeitsstufe. Alle Pixel > 0 sollen zum Vordergrund gehören.

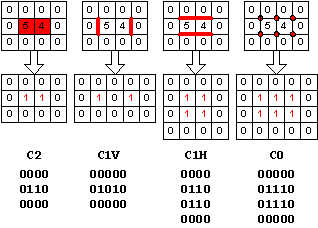C2 = Matrix der C2-Zellen = Pixelmatrix: im Vordergrund ein waagrechtes Gebiet der Fläche 2 allseitig umgeben vom Hintergrund. C1V = Matrix der vertikalen C1-Zellen = Matrix der vertikalen Cracks: codiert linke und rechte Seitenwand des Gebiets C1H = Matrix der horizontalen C1-Zellen = Matrix der horizontalen Cracks codiert die 2 Dächer und die 2 Böden des Gebiets. C0 = Matrix der C0-Zellen = Matrix der Eckpunkte codiert die 3 oberen Dachpunkte und die 3 unteren Bodenpunkte.

    1030       0010        00110        0010       00110
B = 1456; C2 = 0111; C1V = 01001; C1H = 0101; C0 = 01111;
    1300       0100        01100        0011       01111
                                        0100       01100

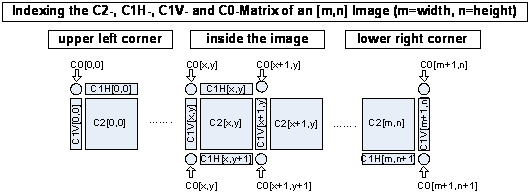
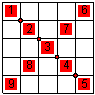Die vier Matrizen C2, C1V, C1H, C0 ersetzen die pauschale Vereinbarung einer 4er oder 8er Nachbarschaft. Wenn eine C0-Zelle zwischen zwei über Eck stehenden C2-Zellen eine Eins enthält, dann sind die beiden C2-Zellen verbunden, falls sie eine Null enthält, sind sie getrennt. Beispiel: Die Pixel 1,2,3,4,5 hängen zusammen, weil es einen Weg über C0-Zellen gibt von 1 nach 5. Sie bilden ein Gebiet. Aber die Pixel 6,7,8 und 9 stehen unzusammenhängend einzeln im Raster, weil sie nicht durch C0-Zellen verbunden sind.

Problem 1: Da die Graphikkarte normalerweise die C2-Matrix im Video-Memory hat, sind die C0-Zellen unsichtbar und der Betrachter kann nur seiner Anschauung folgen, die ihm suggeriert, dass im obigen Beispiel alle Pixel 1 bis 9 zusammenhängen. (Intuitive pauschale 8er Nachbarschaft)
Problem 2: Folgt man der Theorie, benötigt man zur vollständigen und widerspruchsfreien Codierung von Gebietsbegrenzungen den exorbitanten Speicherplatz von 4 Matrizen. Lösung: Man erzeugt nur die Matrizen, die unbedingt nötig sind und nicht immer alle vier. In der Regel ist das nur die C2-Matrix und für den Chain-Code-Startpunktfinder (siehe unten) die C1V-Matrix.
Die C0-Matrix ersetzt man in der Regel durch die pauschale Vereinbarung der 4er oder der 8er Nachbarschaft. Ist nichts vereinbart, dann gilt stillschweigend die 8er Nachbarschaft.
Problem 3: Die Matrizen haben ungleiche Spalten- und Zeilenzahl. Zur Codierung der Cracks und Points am rechten und unteren Bildrand benötigt die C1V-Matrix eine zusätzliche Spalte, die C1H-Matrix eine zusätzliche Zeile und die C0-Matrix beides. Lösung: Man löscht die letzte Spalte und Zeile des Originalbildes (d.h. man setzt deren Grauwerte auf Hintergrund). Dadurch können keine Gebietsbegrenzungen am rechten und unteren Bildrand auftreten und man kann die zusätzlichen Spalten und Zeilen in C1V, C1H und C0 weglassen, weil sie sowieso nur Nullen enthalten würden.

Falls eine pauschale Nachbarschaft (4er oder 8er) vereinbart ist, dann besitzt jede der 4 Matrizen die gleiche Informationsmenge. Man kann dann jede der Matrizen aus jeder anderen erzeugen. Das ist sinnvoll, wenn man die Grenzen von Gebieten sehen will. C1V-, C1H- und C0-Matrizen kann man genau wie C2-Matrizen ins Video-Memory einer Graphikkarte laden und sieht dann unmittelbar und korrekt die Begrenzungen.

Sie finden eine Bauanleitung zum Thema Zellenkomplex unter ../../../C_CVCis/C1_Cells/CVCisCells_d.htm,
oder Sie können eine lauffähiges EXE downloaden: ../../../C_CVCis/C1_Cells/CVCisCells.exe.

Der alte Kettencode = Freeman Code: falsch aber populär

Beispiel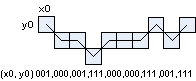

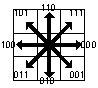
Der Freeman code = Chain Code mit 8 Richtungen ist populär seit 1970. Er kodiert Pixelketten durch x- und y-Koordinate des Startpixels plus eine Kette von 8 Richtungen zu den Nachfolgepixeln. Richtungscode: von 0 Grad im Uhrzeigersinn in 45 Grad-Schritten: 000,001,010,011,100,101,110,111.

Vorteil des Freeman-Code: Redundanzarme Kodierung von Gebietsbegrenzungen durch Pixelketten
Problem: Pixelketten widersprechen der Berandungsrelation und sind damit generell ungeeignet zur Kodierung von Gebietsbegrenzungen aus folgenden Gründen:

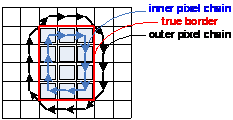Beispiel: Berandung eines 3x4 Rechtecks durch den Freeman-Code Problem 1: Pixel haben Flächen, richtige Grenzlinien müssen aber linienhaft und flächenlos sein. Problem 2: Der richtige Gebietsrand (rot) liegt zwischen einer inneren und einer äußeren Pixelkette. Es ist unklar, welche der beiden Pixelketten den Rand am ehesten repräsentiert. Problem 3: Es ist unklar, was der innere und äußere Rand kleiner Gebieten sein soll (etwa der Rand eines einzelnen Pixels). Problem 4: Es ist unklar, wo die äußere Pixelkette verlaufen soll, wenn ein Gebiet den Bildrand berührt.

Zusammenfassung: Der Freeman-Code ist obsolet und sollte überall durch den Chain Code mit 4 Richtungen = Crack Code ersetzt werden.
Siehe nächstes Kapitel ../CrackCode/CrackCode_d.htm

top of page: