
Computer Vision, Chapter 3: Raster to Vector Conversion
Copyright © by V. Miszalok, last update: 2011-03-11
Let me know
what you think
| Home | Index of Lectures | << Prev | PDF Version |
 |
Computer Vision, Chapter 3: Raster to Vector ConversionCopyright © by V. Miszalok, last update: 2011-03-11 |
 Let me know what you think |
|
Man kann leicht einen Chain-Code (x0,y0)cracks[0 .. no-1] in ein geschlossenes Polygon p der Länge no+1 umwandeln mit folgendem Algorithmus:
ArrayList p = new ArrayList();
p.Add( new Point( x0,y0 ) );
Int32 i, x=x0, y=y0;
for ( i=0; i < no-1; i++ )
{ switch ( cracks[i] )
{ case 'e': x++; break;
case 's': y++; break;
case 'w': x--; break;
case 'n': y--; break;
}
p.Add( new Point( x,y ) );
}
p.Add( new Point( x0,y0 ) );
Man unterdrückt die kolinearen Punkte, wenn man die Zeile nach der switch-Klammer:
Man erhält dann nur dort Eckpunkte, dort wo der Code die Richtung wechselt.
Vorteil: Weniger Redundanz auf horizontalen und vertikalen Strecken.
Nachteil: Verlust der Äquidistanz zwischen den Vertices.
Beispiele:
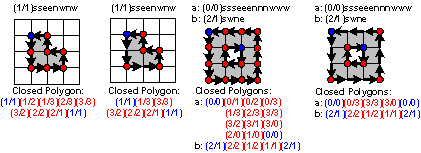
Sie finden eine Bauanleitung zu diesem Thema unter
../../../C_CVCis/C3_Polygon/CVCisPolygon_d.htm,
oder Sie können eine lauffähiges EXE downloaden:
../../../C_CVCis/C3_Polygon/CVCisPolygon.exe.
Die obigen Polygone sind "übergenau" in dem Sinne, dass sie exakt den Kanten jedes einzelnen Berandungspixels folgen. Sie enthalten damit eine unerwünschte "Eckigkeit" und außerdem unerwünschte Redundanz.
Die Aufgabe, diese Eckigkeit und Redundanz unter Beibehaltung der Polygonform zu vermindern, lässt sich so formulieren: Verringere die Zahl der Polygonecken so weit wie möglich, aber sorge dafür, dass keine der verschwindenden Ecken weiter als eine fest vorgegebene Strecke "epsilon" von einer der neuen Kanten entfernt liegt.
Ein einfaches und populäres Verfahren ist der so genannte Gummiband- (= rubber band) Algorithmus:
1) Gummiband am aktuellen Point befestigen.
2) Zum nächsten Point gehen, Gummiband streckt sich.
3) Die Abstände aller rückwärtigen Points zum Gummiband berechnen. Ist jeder einzelne Abstand kleiner gleich epsilon, dann weiter bei 2) falls nicht, gehe zum vorletzten Point zurück und weiter bei 1).
Effizientere (und komplexere) Verfahren siehe: ../kovalevski.pdf (206 KB) Kapitel 5.
PointF p1[polygon_length], p2[polygon_length];
/* p1[i] is the old, redundant polygone, p2[j] the new, shorter one */
int condense_polygon ( float epsilon )
{ int i = 0, j = 0, start = 0, stop;
float px, py, qx, qy, tx, ty, F, square_eps = epsilon * epsilon, comparator;
p2[0].x = p1[0].x;
p2[0].y = p1[0].y;
for ( stop = start + 2; stop < polygon_length; stop++ ))
{ px = p1[start].x; qx = p1[stop].x; dx = qx - px;
py = p1[start].y; qy = p1[stop].y; dy = qy - py;
comparator = square_eps * ( dx * dx + dy * dy );
for ( i = start + 1; i < stop; i++ ))
{ tx = p1[i].x; ty = p1[i].y;
F = px*(qy-ty)+qx*(ty-py)+tx*(py-qy);
if ( F * F > comparator ) /* F*F/d*d > square_eps ? */
{ start = stop -1;
j++;
p2[j].x = p1[start].x;
p2[j].y = p1[start].y;
break;
}
}
}
return j;
}
Abstand eines Punktes T von der Geraden PQ: |
Der Algorithmus beruht auf der Formel für die Fläche eines Dreiecks und folgender Überlegung: Gegeben: eine Strecke d von P(px,py) nach Q(qx,qy) und ein außerhalb liegender Punkt T(tx,ty). Gesucht: Abstand a von T zu d. |
Sie finden eine Bauanleitung zu diesem Thema unter ../../../C_CVCis/C3_Polygon/CVCisPolygon_d.htm,
oder Sie können eine lauffähiges EXE downloaden: ../../../C_CVCis/C3_Polygon/CVCisPolygon.exe.
Gegeben sei ein Polygon (x0,y0)(x1,y1)....(xn-1,yn-1).
Es gibt ein Polynom n-ten Grades das exakt durch alle Punkte des Polygons verläuft:
y = an-1*xn-1 + an-2*xn-2 + an-3*xn-3 + ..... + a2*x2 + a1*x + a0
Durch Einsetzen der n Punkte in die Polynomgleichung bekommt man n lineare Gleichungen mit n Unbekannten a0 bis an-1, woraus sich die ai nach dem Gaußschen Eliminationsverfahren berechnen lassen.
Beispiel:
Polygon mit 5 Ecken (n=4) (0,0)(1,3)(2,0)(3,0)(4,0) ergibt 5 lineare Gleichungen, aus denen sich die 4 unbekannten Koeffizienten a0 bis a4 berechnen lassen:
0 = a4*0*0*0*0 + a3*0*0*0 + a2*0*0 + a1*0 + a0
3 = a4*1*1*1*1 + a3*1*1*1 + a2*1*1 + a1*1 + a0
0 = a4*2*2*2*2 + a3*2*2*2 + a2*2*2 + a1*2 + a0
0 = a4*3*3*3*3 + a3*3*3*3 + a2*3*3 + a1*3 + a0
0 = a4*4*4*4*4 + a3*4*4*4 + a2*4*4 + a1*4 + a0
Lösung: a4 = -0,5; a3 = +4,5; a2 = -13; a1 = +12; a0 = 0
und y = -0,5*x4 + 4,5*x3 - 13*x2 + 12*x
Überbrückung des Zwischenraums zwischen 2 Punkten:
Man stelle sich vor, dass je 2 Punkte eines Polygons durch eine Eisenbahnlinie verbunden seien. Die Geschwindigkeit der Züge sei so eingerichtet, dass (unabhängig von der Streckenlänge) die Fahrzeit zwischen zwei aufeinander folgenden Punkten P(i) und P(i+1) immer exakt 1 Stunde betrage. Dann kann man die aktuelle Position x(i,t),y(i,t) des Zuges exakt angeben durch die Zeit t mit 0 <= t < 1, die seit der Abfahrt von P(i) vergangen ist:
x(i,t) = x(i) + t*(x(i+1)-x(i)) = x(i) - t*x(i) + t*x(i+1) = (1-t)*x(i) + t*x(i+1)
y(i,t) = y(i) + t*(y(i+1)-y(i)) = y(i) - t*y(i) + t*y(i+1) = (1-t)*y(i) + t*y(i+1)
Die beiden Gleichungen kann in Kurzschreibweise so zusammenfassen:
P(i,t) = P(i) + t*(P(i+1)-P(i)) = P(i) - t*P(i) + t*P(i+1) = (1-t)*P(i) + t*P(i+1)
Überbrückung des Zwischenraums zwischen 3 Punkten
Man stelle sich vor, dass 2 Züge auf 2 aufeinander folgenden Polygonstrecken gleichzeitig abfahren:
Zug1 von P(i ) nach P(i+1) mit P(i ,t) = (1-t)*P(i ) + t*P(i+1)
Zug2 von P(i+1) nach P(i+1) mit P(i+1,t) = (1-t)*P(i+1) + t*P(i+2)
Von Zug1 starte ein Hubschrauber sofort bei Abfahrt in Richtung Zug 2. Der Hubschrauber richte seine Geschwindigkeit so ein, dass er exakt eine Stunde bis zur Landung auf Zug2 brauchen wird. Er fliegt nach Sichtverbindung auf Zug2 (und nicht etwa auf Punkt P(i+2)) zu.
Zur Unterscheidung der Wege der Züge (= 1. Überbrückung) und des Wegs des Hubschraubers (= 2. Überbrückung) nehmen wir eine Umbenennung vor:
P(i,t) → P(1,i,t) und P(i+1,t) → P(1,i+1,t)
P(2,i,t) sei der Flugweg des Hubschraubers von P(1,i,t) nach P(1,i+1,t):
P(2,i,t) = (1-t)* P(1,i,t) + t* P(1,i+1,t)
= (1-t)*((1-t)*P(i) + t*P(i+1)) + t*((1-t)*P(i+1) + t*P(i+2))
= (1-t)* (1-t)*P(i) + 2*t*(t-1)*P(i+1) + t*t*P(i+2).
Weil (t-1)*(t-1), t*(t-1) und t*t vorkommen, ist diese Flugbahn eine Parabel (=Polynom 2. Grades) vom Typ P(2,i,t) = A*t*t + B*t + C.
Überbrückung des Zwischenraums zwischen 4 Punkten
Man stelle sich vor, dass 3 Züge und 2 Hubschrauber gleichzeitig starten. Man stelle sich weiterhin vor, dass sofort vom 1. Hubschrauber eine Brieftaube zum 2. Hubschrauber los fliege. Die Taube fliegt nach Sichtverbindung immer auf Hubschrauber 2 zu und sie richtet ihre Fluggeschwindigkeit so ein, dass sie exakt eine Stunde brauchen wird, bis zur Landung auf Hubschrauber 2. Die Flugbahn der Taube ist dann ein Polynom 3. Grades vom Typ P(3,i,t) = A*t*t*t + B*t*t + C*t + D.
Überbrückung des Zwischenraums zwischen n+1 Punkten
Wenn n+1 Polygonpunkte gegeben sind, dann kann man eine Polynom n-ten Grades errechnen durch
n-maliges sukzessives Anwenden der Formel P(r,i,t) = (1-t)*P(r-1,i,t) + t*P(r-1,i+1,t) mit r = 1.....n und
i = 1....n-r. Dieses letzte Polynom n-ten Grades heißt Bézier-Kurve des Polygons.
| top of page:
|