
Fourier Transformation
Copyright © by V. Miszalok and F. Reuß , last update: 2011-03-09

Let me know
what you think
| Home | Index of Lectures | PDF Version of this Page |
 |
Fourier TransformationCopyright © by V. Miszalok and F. Reuß , last update: 2011-03-09 |
 Let me know what you think |
Satz von Jean Baptiste Joseph Baron de Fourier (1768-1830) in: Théorie analytique de la chaleur, Paris 1822:
Durch einfache Summierung einer Konstanten und von Cosinus- und Sinus-Schwingungen lässt sich jede beliebige periodische Funktion f(x) beliebig genau annähern.
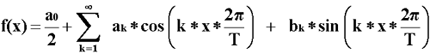
Diese Summe nennt man Fourierreihe. Die Darstellung einer beliebigen periodischen Funktion in Form dieser Reihe nennt man Fourierzerlegung oder harmonische Analyse.
Um Schreibarbeit in den Punkten (1) bis (4) zu sparen, stauchen/dehnen wir die x-Achse willkürlich so, dass T immer exakt gleich 2*Pi ist.
Die Summanden der Fourierreihe ergeben sich dann so:
(1) Man fängt an mit einer Konstanten, nämlich der Hälfte des Mittelwertes von f(x) = a0/2.
(2) Nehmen wir an, die periodische Funktion habe die Periode T, dann muss man zur Konstanten je eine Cosinus- und Sinus-Schwingungen addieren, die beide ebenfalls die Periode T haben (Grundschwingung) mit den noch unbekannten Amplituden a1 für den Cosinus und b1 für den Sinus:
f(x) = a0/2 +a1*cos(x) + b1*sin(x).
(3) Danach addiert man je einen Cosinus und Sinus mit halber Periode =T/2 und den (noch unbekannten) Amplituden a2 und b2:
f(x) = a0/2 +a1*cos(x) + b1*sin(x) + a2*cos(2*x) + b2*sin(2*x).
(4) dann je einen weiteren mit Periode =T/3 und den (noch unbekannten) Amplituden a3 und b3 und so weiter mit Perioden, die ganzzahlig immer weiter geteilt sind T/4, T/5 usw.
In der Formel tauchen die Teiler von T in Form des Faktors k auf: x*2*Pi / (T/k) = k*x*2*Pi/T, weil Teilung von T durch k gleichbedeutend mit Erhöhung der Frequenz um den Faktor k ist.
k dient in der Formel nicht nur als Frequenzvervielfacher sondern gleichzeitig als Zählindex der gesamten Summation und als Numerierungsindex der unbekannten Amplitudenwerte.
siehe auch: http://de.wikipedia.org/wiki/Fourier-Transformation
Fourier, der Physiker war, wurde zu diesem Satz durch physikalische Experimente inspiriert.
Beispiel 1: Es ist kein Problem, beliebig schräge und schrille Geräusche mit Saiteninstrumenten hervorzubringen, obwohl deren Saiten nur und ausschließlich harmonisch schwingen können. Ein Gemisch reiner Frequenzen ergibt in der Regel eine unreine Dissonanz (und nur selten einen Klang).
Fouriers intuitiver Umkehrschluß, dass nämlich jedwedes unreine Ergebnis als Summation reiner Schwingungskomponenten aufgefasst werden kann, hat sich als richtig und außerordentlich fruchtbar erwiesen.
Beispiel 2: In der Gehörschnecke = Cochlea des Innenohres befindet sich ein fluid-mechanisches System mit definiert geordneten Resonatorpunkten. Sensorzellen (Haarzellen mit bewegungsempfindlichen Zellfortsätzen = Zilien) messen dort die Auslenkung der Resonatormembran. Verzögerungsfrei synchron mit dieser Auslenkung ändert sich das Zellwandpotential der Haarzellen ähnlich wie die Ausgangsspannung eines Mikrophons und die Haarzelle schüttet Neurotransmitter in den Extrazellulärraum aus. Dieser triggert die Auslösung von Nervenimpulsen in exakt einer Faser des Hörnerven. Eine Faser des Hörnerven transportiert somit Information über die aktuelle Amplitude genau einer einzigen charakteristischen Frequenz.
Beispiel 3: Ein Schwingkreis aus Spule und Kondensator hat eine bestimmte Resonanzfrequenz. Er "erkennt" in jedem Frequenzgemisch das Vorhandensein oder Nichtvorhandensein seiner eigenen Frequenz und gerät in Resonanz = Mitschwingung, falls seine Eigenfrequenz vorhanden ist. Man darf sich dieses "Erkennen" nicht als aktiven Prozess vorstellen, sondern man sollte ihn als zwanghaftes "in Resonanz geraten" denken.
Diese Resonanz von Schwingkreisen ist die Grundlage der elektrischen Tontechnik. Man exponiert eine wohlgeordnete Reihe von Schwingkreisen einem beliebigen Signal und verstärkt die Resonanzantworten soweit diese überhaupt vorhanden sind. Diese Antwortsignale mischt man wieder und das Ergebnis ist ein verstärktes Signal, das selbstverständlich nur aus denjenigen reinen Frequenzen zusammengesetzt ist, für die Resonatoren vorhanden waren.
Die erstaunliche Erfahrung ist, dass man mit relativ wenig Resonatoren beliebige Schwingungen realitätsnah verstärken kann.
Beispiel 4: Pendel sind strikt monofrequent. Will man einem Pendel größere Amplitude oder einem Kind auf einer Schaukel größeren Spaß verschaffen, dann muss die Energie in Resonanz mit der Pendelbewegung zugeführt werden. Es ist unmöglich, aufschaukelnde Bewegungsenergie kontinuierlich oder in einer anderen als der Pendelfrequenz zuzuführen.
Zusammenfassung: Fouriertransformation bedeutet die Zerlegung beliebiger periodischer Schwingungen in eine endliche oder unendliche Summe frequenzreiner Schwingungen durch frequenzreine Resonatoren und die Umkehrung des Vorgangs, nämlich der Rekonstruktion beliebiger periodischer Signale durch Addition harmonischer Resonatorschwingungen.
Zu diesem Zweck benötigt man mathematische "Resonatoren", die in Analogie zu einem Schwingkreis feststellen können, ob eine bestimmte Frequenz in einem Gemisch vorhanden ist und wenn ja in welchem Verhältnis sie zum Gesamtsignal des Gemischs beiträgt.
Zwecks Schreibvereinfachung stauchen/dehnen wir wieder T auf die Länge 2*Pi.
Joseph Fouriers geniale Idee ist folgende:
(1) Er multipliziert das Originalsignal mit den reinen Resonatorsignalen cos(k*x) und sin(k*x). Er erhält für jedes k zwei Produktsignale f(x)*cos(k*x) und f(x)*sin((k*x) mit folgenden Eigenschaften: Die Produktfunktionen haben immer positive und negative Werte, auch dann, wenn das Originalsignal nur positiv oder nur negativ war. Die Produktfunktionen sind hoch positiv dort, wo Berg auf Berg und wo Tal auf Tal trifft (=Fall 1) und hoch negativ dort wo Berg auf Tal trifft (=Fall 2).
Tritt in f(x)*cos(k*x) Fall 1 ungefähr gleich oft auf wie Fall 2, dann haben f(x) und cos(k*x) nichts gemeinsam.
Tritt in f(x)*sin(k*x) Fall 1 ungefähr gleich oft auf wie Fall 2, dann haben f(x) und sin(k*x) nichts gemeinsam.
Tritt in f(x)*cos(k*x) Fall 1 viel öfter auf als Fall 2 oder Fall 2 viel öfter als Fall 1 , dann haben f(x) und cos(k*x) die Frequenz k gemeinsam.
Tritt in f(x)*sin(k*x) Fall 1 viel öfter auf als Fall 2 oder Fall 2 viel öfter als Fall 1 , dann haben f(x) und sin(k*x) die Frequenz k gemeinsam.
(2) Ausgehend von diesen Überlegungen benutzt Fourier die von den Produktfunktionen eingeschlossenen Flächen als Resonatoren: Diese Flächen werden berechnet durch die Integrale über f(x)*cos(k*x)*dx entlang einer Periode T.
Teilt man die Flächen = Integrale durch T, dann erhält man die normierten Resonanzantworten, die sogenannten Fourierkoeffizienten, nämlich 2 Antworten ak und bk pro untersuchter Resonanzfrequenz k:
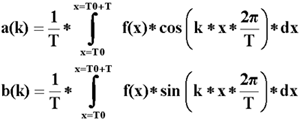
| f(x) = 3 sinus curves hidden under severe noise |
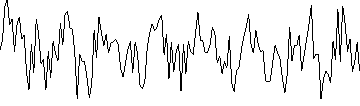 |
| ak+bk amplitudes after fourier transform |
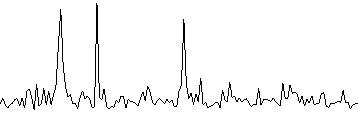 |
Warum benötigt Fourier zwei Resonatoren (Cosinus und Sinus) pro Frequenz ? Warum genügt nicht einer von beiden ?
Antwort: Trifft in der Produktfunktion ein Berg von f(x) auf einen Nulldurchgang von cos(k*x), dann wird der Berg in eine positive und in eine negative Hälfte geteilt die sich auch dann zu Null summieren, wenn f(x) und cos(k*x) gleichfrequent sind. Fourier braucht für diesen Fall einen Zwillings-Resonator gleicher Frequenz, der um 90 Grad phasenverschoben ist. Dieser gleichfrequente Bruderresonator schwingt, weil er in Phase mit dem Signal ist.
Physikalische Resonatoren wie die Schwingkreise in Beispiel 2 benötigen das nicht. Ohne Erregung befinden sie sich in Ruhe, sie schwingen nicht selbstständig, sie geraten erst langsam in Resonanz und schwingen sich ein in Phase mit ihrer Erregerfrequenz.
Die Fourierresonatoren schwingen aber immer und selbstständig, sie sind unfähig, sich auf eine fremde Phasenlage einzustellen.
Sie haben den Charakter von immer vorhandenen Testsignalen, die mit Erregerwellen Produkte und Produktintegrale bilden und man braucht (mindestens) zwei um 90 Grad phasenverschobene Testsignale um sicher zu gehen, dass eines davon in Phase mit f(x) ist.
Wir werden weiter unten sehen, dass wenn man f(x) in eine definiere Phasenlage zwingen kann, tatsächlich ein Fourierresonator genügt (i.a. Cosinus).
Fourier konstruiert aus der Grundfrequenz 2*Pi/T für jedes ganzzahlige Frequenzvielfache je 2 Resonatoren und probiert die Resonatoren schlicht alle aus. Die Probe besteht jeweils aus Multiplikation von Resonator und Signal und Integration des Multiplikationsergebnisses. Wenn sich in den Integralen positive und negative Flächen zu Null kompensieren, dann ist das jeweilige Testergebnis negativ, andernfalls positiv. Das Vorgehen von Fourier ist keinesweg elegant, sondern brute force Büffeltaktik. Der Rechenaufwand ist exorbitant und nur von Maschinen zu leisten.
In vorherigen Absätzen haben wir in der Tradition des 19. Jahrhunderts Begriffe aus Mathematik und Physik parallel und synonym benutzt.
Die physikalische Sprechweise ist bei weitem einfacher und intuitiver, die mathematische ist abstrakter aber deshalb breiter verwendbar.
Man sollte beide analoge Begriffswelten beherrschen und zweckmäßig anwenden.
Analogie der harmonischen Zusammensetzung = harmonische Synthese:
Physik: Superposition = Man kann jede beliebige Schwingung durch Superposition reiner Schwingungen zusammensetzen.
Mathematik: Summation = Man kann jede beliebige periodische Funktion durch addieren von Cosinus- und Sinusfunktionen beliebig genau approximieren.
Analogie der Ganzzahligkeit:
Physik: Jede beliebige Schwingung läßt sich zusammensetzen aus einer Grundschwingung und ganzzahligen Frequenzvielfachen davon = Oberwellen.
Beispiel: Eine zwischen zwei Fixpunkten eingespannte Geigensaite kann nur in ganzzahligen Vielfachen ihrer Grundfrequenz schwingen, weil an den Einspannpunkten keine Auslenkung möglich ist.
Jedes noch so schräge oder schrille Geräusch der Saite kann also nur aus der Grundfrequenz und ganzzahligen Vielfachen davon bestehen.
Man kann unmöglich das Geräusch durch nichtganzzahlige Vielfache der Grundfrequenz (etwa 2,2- oder 7,5-fache) zusammensetzen, weil solche Schwingungen die Saite aus dem hinteren Einspannpunkt reißen müßten.
Mathematik: Jede beliebige periodische Funktion f(x) ist ein Punkt im orthogonalen normierten Vektorraum, der durch die orthogonalen Basisvektoren cos(k) und sin(k) aufgespannt wird.
Analogie der harmonischen Zerlegung = harmonische Analyse:
Physik: Jede Schwingung lässt sich durch Resonatoren in ihre Bestandteile zerlegen. Man benötigt exakt so viele Resonatoren wie reine Schwingungen vorhanden sind und diese Resonatoren müssen schmalbandig exakt in ganzzahligen Vielfachen der Grundfrequenz resonanzfähig sein.
Mathematik: Die Fouriertransformation ist die Faltung = Convolution von f[x] mit cosinus(k*arg) und sinus(k*arg) für jedes ganzzahlige Vielfache von arg und liefert die orthogonalen Koordinaten ak und bk.
diverse weitere Analogien:
| physikalische Sprechweise | mathematische Sprechweise |
| Zeit t | unabhängige Variable x |
| Auslenkung(t), Schalldruck(t), Feldstärke(t) | Funktionswert y = f(x) |
| Schwingungsdauer der Grundwelle T | Periode L = 2*Pi/T |
| Oberwellen der Wellenlängen T/2, T/3, T/4 etc. | Reskalierung durch Multiplikation der Periode mit 2, 3, 4 etc. |
| Resonator für die k-te Oberwelle | Basisvektoren cos(k*L) und sin(k*L) |
| Resonanzantwort am k-ten Resonator | Faltung = Convolution der cos und sin mit f(x) ergeben ak und bk |
| Ruhelage | Nulllinie, Mittelwert, a0/2 |
| Amplitude der Grundwelle | Wurzel aus (a1*a1 + b1*b1) |
| Amplitude der k-ten Oberwelle | Wurzel aus (ak*ak + bk*bk) |
Die häufigste Speicherform von Funktionen in Computern sind diskrete äquidistante Daten in Form eindimensionaler Arrays (z.B. Fieberkurven, Börsenkurse, Pixel in Zeilen und Spalten).
Es hat sich herausgestellt, dass so gut wie alle solche Daten Wellenform d.h. Periodizität haben und dass die Fouriertransformation ideal geeignet ist, unerwünschte Wellen aus den Daten zu entfernen mit dem Ziel der Redundanzvernichtung und Kompression. An so etwas hat Joseph Fourier nie auch nur im Traum gedacht, aber heute ist dies die bei weitem wichtigste Anwendung seiner harmonischen Analyse.
Die Überführung der Rechenvorschriften Fouriers für ak und bk auf diskrete Daten ist einfach:
Liegt das Signal f(x) vor in Form eines Arrays der Länge N, dann übernimmt N die Rolle der Periodendauer T.
Jeder Resonator nimmt nun auch die Form eines Arrays der Länge N an.
Summen von 0 bis N-1 ersetzen die Integrale von To bis To+T.
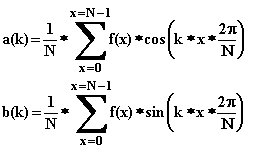
Da wir N Cosinus- und N Sinus- Resonatoren brauchen, legen wir die Resonatoren zweckmäßig in Form von 2 quadratischen N*N-Matrizen an.
Produktbildung und Summierung geschehen nunmehr in Form einer vektoriellen Multiplikation von f(x) mit allen Zeilen beider Matrizen.
Die ak und bk ergeben sich als die N + N Skalarprodukte: f(x) jeweils vektoriell multipliziert mit einer Matrixzeile dividiert durch N.
Der Rechenaufwand an Gleitkommaoperationen ist hoch:
N*N Berechnungen von Cosinus plus N*N Berechnungen von Sinus plus 2*N*N Multiplikationen plus 2*N*N Additionen plus 2*N Divisionen.
| Beispiel einer Fourierzerlegung eines Signals mit N=4 |
 |
C# Programm für dieses N=4 Beispiel
using System;
using System.Drawing;
using System.Windows.Forms;
using System.Text;
public class Form1 : Form
{ [STAThread] static void Main() { Application.Run( new Form1() ); }
const int N = 4;
float[] f0 = { 1f, 0f, 2f, 1f }, f1 = new float[N];
float[,] cos = new float[N,N] , sin = new float[N,N];
float[] a = new float[N] , b = new float[N];
StringBuilder sb = new StringBuilder();
public Form1()
{ Text = "Prof. Miszalok's Fourier sample with N=4";
Width = 320; Height = 400;
int x, k;
for ( k=0; k < N; k++ ) //prepare resonators
for ( x=0; x < N; x++ )
{ cos[k,x] = Convert.ToSingle( Math.Cos( k*x*Math.PI/2.0 ) ) ;
sin[k,x] = Convert.ToSingle( Math.Sin( k*x*Math.PI/2.0 ) ) ;
}
for ( k=0; k < N; k++ ) //Fourier transform
{ for ( x=0; x < N; x++ )
{ a[k] += f0[x] * cos[k,x]; //convolution
b[k] += f0[x] * sin[k,x]; //convolution
}
a[k] /= N; b[k] /= N; //normalisation
}
for ( k=0; k < N; k++ ) //back transform
for ( x=0; x < N; x++ ) { f1[x] += a[k]*cos[k,x] + b[k]*sin[k,x]; }
//compose output string
sb.Append ("f0:\r\n");
for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,5:F0}", f0[x]) );
sb.Append( "\r\ncos:\r\n" );
for ( k=0; k < N; k++ )
{ for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,5:F0}", cos[k,x]) );
sb.Append( "\r\n" );
}
sb.Append( "sin:\r\n" );
for ( k=0; k < N; k++ )
{ for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,5:F0}", sin[k,x]) );
sb.Append( "\r\n" );
}
sb.Append( "a:\r\n" );
for ( k=0; k < N; k++ ) sb.Append( String.Format( "{0,9:F2}", a[k] ) + "\r\n" );
sb.Append( "b:\r\n" );
for ( k=0; k < N; k++ ) sb.Append( String.Format( "{0,9:F2}", b[k] ) + "\r\n" );
sb.Append( "f1:\r\n" );
for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,5:F0}", f1[x]) );
sb.Append( "\r\n" );
}
protected override void OnPaint( PaintEventArgs e )
{ e.Graphics.DrawString( sb.ToString(), Font, new SolidBrush( Color.Red ), 0, 0 ); }
}
The following C#-program
1) fills an array f0 with 3 frequencies,
2) computes the ak and the bk,
3) transforms them back into an array f1,
4) makes an output string and displays it,
5) reduces memory to 50% and computing time to 30% compared with the raw Fourier formula.
The program derives advantage from inherent Fourier symmetry and limits (without any loss of precision) the no.s of ak and bk to N/2+1. Reason: The original f[x] has N elements and when both the ak and the bk have N elements, there must be a redundancy of 50%. Indeed, the high numbered ak and bk with k > N/2 mirror the low numbered with k < N/2 in the following way:
1) when N is even: a0,...,aN/2, aN/2-1, aN/2-2,...,a1. Sample N=8: a,b,c,d,e,d,c,b
2) when N is odd : a0,...,aN/2, aN/2, aN/2-1, aN/2-2,...,a1. Sample N=9: a,b,c,d,e,e,d,c,b
Conclusion: There is no need to compute more than N/2+1 ak and bk. It follows that the cos[,] and sin[,] resonator matrices don't need to be quadratic: N/2+1 rows (with N columns each) are sufficient.
There is another interesting symmetry inside the remaining resonator matrices: The upper right half is identical to the lower left half with diagonal symmetry because cos(k*x*arcus) is identical with cos(x*k*arcus) and same with sin(...). Therefore it's possible to compute the upper right corner and to mirror the values to down left.
Further accelerations:
1) We set the first row and column of cos(k*x*arcus) always to 1f and of sin(k*x*arcus) always to 0f without any computation.
2) We set a0 always to the average of f[x] and b0 always to 0f without any convolution.
The disadvantages of these accelerations are:
1) The code is more complex than before.
2) The normalisation becomes tricky compared to the Fourier formula: We have to double all ak and bk except a0,b0 and aN/2,bN/2.
Summary: An optimized Fourier transform can be surprisingly fast. In cases with N < 1000 there is no need to use any Fast Fourier Transform FFT with its multiple restrictions and inaccuracies.
using System;
using System.Drawing;
using System.Windows.Forms;
using System.Text;
public class Form1 : Form
{ [STAThread] static void Main() { Application.Run( new Form1() ); }
const int N = 16;
float[] f0 = new float[N] , f1 = new float[N]; //input, output
float[,] cos = new float[N/2+1,N], sin = new float[N/2+1,N];//resonators
float[] a = new float[N/2+1] , b = new float[N/2+1]; //Fourier coefficients
StringBuilder sb = new StringBuilder(); //one string takes all
public Form1()
{ Text = "Prof. Miszalok's Fourier sample with N=16";
Width = 500; Height = 600;
int x, k;
double arcus = 2*Math.PI/N, k_arcus, x_k_arcus;
for ( x=0; x < N; x++ ) //input = mixture of 3 frequencies, just for fun
{ f0[x] = (float)Math.Cos( x * arcus );
f0[x] += (float)Math.Sin( 3 * x * arcus );
f0[x] += (float)Math.Cos( 6 * x * arcus + Math.PI/4 );
}
//prepare resonators
for ( x=0; x < N; x++ ) { cos[0,x] = 1f; sin[0,x] = 0f; } //row no. 0
for ( k=0; k <= N/2; k++ ) { cos[k,0] = 1f; sin[k,0] = 0f; } //column no. 0
for ( k=1; k <= N/2; k++ ) //resonator rows 1 to N/2
{ k_arcus = k * arcus;
for ( x=k; x < N; x++ ) //upper right triangle of cos[,] and sin[,]
{ x_k_arcus = x * k_arcus;
cos[k,x] = Convert.ToSingle( Math.Cos( x_k_arcus ) ) ;
sin[k,x] = Convert.ToSingle( Math.Sin( x_k_arcus ) ) ;
if ( x <= N/2 && k != x ) //mirror to lower left except diagonal
{ cos[x,k] = cos[k,x]; sin[x,k] = sin[k,x]; }
}
}
for ( x=0; x < N; x ++ ) a[0] += f0[x]; a[0] /= N; b[0] = 0f;
for ( k=1; k <= N/2; k++ ) //Fourier transform
{ for ( x=0; x < N; x++ )
{ a[k] += f0[x] * cos[k,x]; //convolution
b[k] += f0[x] * sin[k,x]; //convolution
}
if ( k < N/2 ) { a[k] *= 2f/N; b[k] *= 2f/N; } //doubling and normalisation
else { a[k] /= N; b[k] /= N; } //normalisation
}
for ( k=0; k <= N/2; k++ ) //back transform
for ( x=0; x < N; x++ ) { f1[x] += a[k]*cos[k,x] + b[k]*sin[k,x]; }
//compose output string
sb.Append ("f0:\r\n");
for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,6:F1}", f0[x]) );
sb.Append( "\r\ncos:\r\n" );
for ( k=0; k <= N/2; k++ )
{ for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,6:F1}", cos[k,x]) );
sb.Append( "\r\n" );
}
sb.Append( "sin:\r\n" );
for ( k=0; k <= N/2; k++ )
{ for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,6:F1}", sin[k,x]) );
sb.Append( "\r\n" );
}
sb.Append( "a:\r\n" );
for ( k=0; k <=N/2; k++ ) sb.Append( String.Format( "{0,9:F2}", a[k] ) + "\r\n" );
sb.Append( "b:\r\n" );
for ( k=0; k <=N/2; k++ ) sb.Append( String.Format( "{0,9:F2}", b[k] ) + "\r\n" );
sb.Append( "f1:\r\n" );
for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,6:F1}", f1[x]) );
sb.Append( "\r\n" );
}
protected override void OnPaint( PaintEventArgs e )
{ e.Graphics.DrawString( sb.ToString(), Font, new SolidBrush( Color.Red ), 0, 0 ); }
}
Experiments:
1. Try out the back transform with frequency cuts by replacing the upper limit N/2 of the back transform loop successively by 0,1,2... till 7 and observe how f1[x] comes closer to f0[x].
2. Explain the positions and the signs of the values ak != 0f and bk != 0f.
3. Mix new and higher frequencies into f0 by inserting new lines f0[i] += (float)Math....( ... ); into the first for-loop of the program.
4. Mix 10% noise to f0:
Random r = new Random();
f0[i] += 0.1f * (float)( r.NextDouble()-0.5 );
and limit the back transform to k <= 7.
5. Increase N to N > 20;
6. You will find more programs dealing with Fourier transforms here:
www.miszalok.de/C_CVCis/C6_FourierTransform = Analysis of contours in raster drawings
www.miszalok.de/C_CVCis/C5_FourierRecognition = Learning Optical Character Recognition
Das folgende Demo-Programm wurde geschrieben von Greg Slabaugh, Georgia Tech, Atlanta 1998.
Fourier Demo Applet
siehe englische Version dieser Vorlesung:
Fourier_english.htm#a8
| top of page: |