 |
Image Processing: Filters
1.1. The Average Filter
1.1.1 The 3x3 Average Filter
1.1.2 The fast 5x5 Average Filter
1.2.3 Border Handling
1.1.4 Averaging Real Images
1.1.5 Questions & Answers
Copyright © by V. Miszalok, last update: 2011-07-02 |

Let me know
what you think
|
The 3x3 Average Filter
is the most popular and simple lowpass filter.
It improves noisy images, flattens local differences and reduces sharpness.
It replaces any pixel value by the democratic vote of its 3x3 rectangular neighborhood.
It doesn't filter and has to avoid the border rows and columns where just 6 or (in the edges) 4 neighbors exist.
Here is the pseudo-code for gray value images:
1. Take the pixel's gray value and add the gray values of its eight neighbors,
2. divide the sum by 9, round the result to integer, and
3. write it to the output image at the same x,y position.
******************************************************************************************************
Experiments:
******************************************************************************************************
1. Draw thick objects.
2. Draw objects that touch the image border.
3. Draw parallel thin lines.
4. Draw an arbitrary half side of the canvas in white and observe how the filter changes the sharp edge to a ramp.
******************************************************************************************************
C#-Code of the AverageFilter3x3 click event:
Byte[,] image0 = new Byte[ySize,xSize]; // global input image
Byte[,] image1 = new Byte[ySize,xSize]; // global output image
private void AvFilter3x3_Click( object sender, RoutedEventArgs e )
{ Int32 sum, x, xx, xxx, y, yy, yyy;
for ( y=1; y < ySize-1; y++ ) //for each row except the first and last
{ for ( x=1; x < xSize-1; x++ ) //for each column except the first and last
{ sum = 0;
for ( yy=-1; yy <= 1; yy++ ) //upper, mid and lower indicees
{ yyy = y + yy;
for ( xx=-1; xx <= 1; xx++ )//left, mid and right indicees
{ xxx = x + xx;
sum += image0[yyy,xxx]; //add them up
} //====== end for (int xx... ================
} //======== end for (int yy... ================
image1[y,x] = Convert.ToByte( (float)sum/9f ); //divide by 9 and round
} //============ end for (int x... =====================
} //============== end for (int y... =====================
}
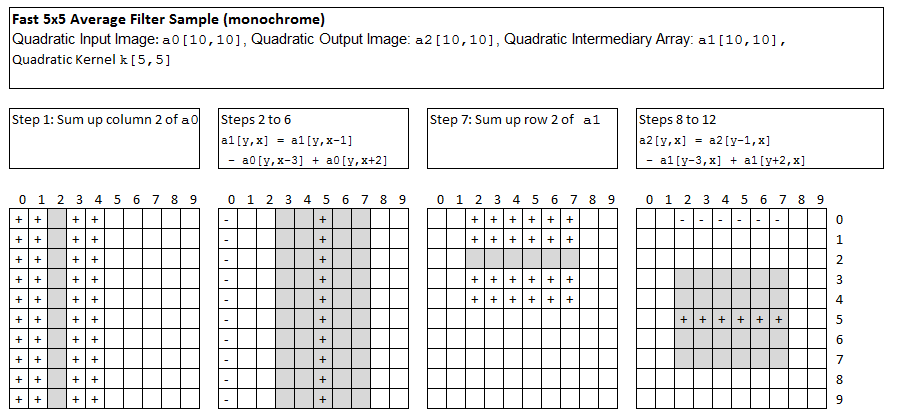
The Fast 5x5 Average Filter
Our monochrome image input is stored in A0[ySize,xSize] and the filtered output should appear in A2[ySize,xSize]
At any step normal 5x5 averaging needs 25 additions. Trick: They can be reduced to 2 subtractions and 4 additions per pixel.
| Idea 1 | Separate the 2D-kernel-wide-sum into two 1D-sums. |
| Idea 2 | Store the result of the first horizontal addition into an intermediary array A1[ySize,xSize]. |
| Idea 3 | In any row y of column 2 of A1 add up 5 values: A1[y,2] = A0[y,0] + A0[y,1] + A0[y,2] + A0[y,3] + A0[y,4]; |
| Idea 4 | At each further horizontal step from x-1 to x use the last A1[y,x-1] to compute the next A1[y,x] = A1[y,x-1] - A0[y,x-3] + A0[y,x+2]. |
| Idea 5 | When A1[ySize,xSize] is complete, add up the vertical 1D-sums using A1[ySize,xSize]. |
| Idea 6 | Use the same trick as with ideas 3+4 vertically.
Add up row 2: A2[2,x] = A1[0,x] + A1[1,x] + A1[2,x] + A1[3,x] + A1[4,x];
and roll down the remaining 5 column with A2[y,x] = A2[y-1,x] - A1[y-3,x] + A0[y+2,x]; |
//C#-Code:
int[,] A0 = new int[ySize,xSize]; //input (can be a Byte array)
int[,] A1 = new int[ySize,xSize]; //intermediary
int[,] A2 = new int[ySize,xSize]; //output (can be a WritebleBitmap image)
private void FastAvFilter5x5()
{ int x, y;
for ( y=0; y < ySize; y++ ) //clear A1 and A2
for ( x=0; x < xSize; x++ ) A1[y,x] = A2[y,x] = 0;
for ( y=2; y < ySize-2; y++ ) //horizontal sums → steps 1 to 6
{ for ( x=0; x < 5; x++ ) A1[y,2] += A0[y,x];
for ( x=3; x < xSize-2; x++ ) A1[y,x] = A1[y,x-1] - A0[y,x-3] + A0[y,x+2];
}
for ( x=2; x < xSize-2; x++ ) //vertical sums → steps 7 to 12
{ for ( y=0; y < 5; y++ ) A2[2,x] += A1[y,x];
for ( y=3; y < ySize-2; y++ ) A2[y,x] = A2[y-1,x] - A1[y-3,x] + A1[y+2,x];
}
for ( y=2; y < ySize-2; y++ ) //divide and round
for ( x=2; x < xSize-2; x++ ) A2[y,x] = Convert.ToInt32( (float)A2[y,x] / 25f );
}
Border Handling
means the method to fill the empty 2 horizontal and 2 vertical border stripes and the 4 edges of the fast average filtered image.
The fast average filter can't populate these borders.
There are three basic methods of border handling:
1. Do nothing. Just don't care of the loss of some rows and columns at the borders.
2. Border handling by copy: Fill the empty border space with the nearest filtered pixel.
3. Border handling by filter: Fill the empty border space by filtering with reduced filter power restricted to the truncated neighborhood.
Method 1 is fast and easy. Loosing some rows and columns at the image borders doesn't matter when big images are filtered by small filter sizes.
But the method isn't feasable with big filters on small images.
Method 2 is a separate process started after completion of filtering:
1. The color values of the first filtered output row kernel.Height/2 are copied up into the empty upper rows.
2. The color values of the last valuable row are copied down into the empty lower rows.
3. The color values of the first valuable column kernel.Width/2 are copied left into the empty leftmost columns.
4. The color values of the last valuable column are copied left into the empty rightmost columns.
5. There is no need to handle the edges separately.
Method 3 is time consuming and delivers good results with small filters.
The method can be incorporated in the simple average filter algorithm and doesn't require a separate process after filtering.
But it's impossible to obtain a homogenously blurred image using big filters of about the image size.
//C#-Code of a 5x5 Border Fill Function:
private void borderHandling5x5()
{ int x, y;
for ( y=0; y < 2; y++ ) //upper border
for ( x=2; x < xSize-2; x++ ) A2[y,x] = A2[2,x];
for ( y=ySize-3; y < ySize; y++ ) //lower border
for ( x=2; x < xSize-2; x++ ) A2[y,x] = A2[ySize-3,x];
for ( x=0; x < 2; x++ ) //left border
for ( y=0; y < ySize; y++ ) A2[y,x] = A2[y,2];
for ( x=xSize-2; x < xSize; x++ ) //right border
for ( y=0; y < ySize; y++ ) A2[y,x] = A2[y,xSize-3];
}
Advantages of method 2 of border handling:
1. All resulting pixels are averaged using the same no. of neighbors, which is mandatory for the fast average algorithm.
2. There is no vanishing filtering power caused by the restricted filter size at the borders.
3. It delivers reasonable results when the kernel is nearly as big as the image itself.
4. When the kernel size is as big as the image size,
the whole image is just averaged once and a homogenous image comes out as expected.
5. It is the fastest possible way of border handling.
6. Interesting side effect: Filtering becomes faster and faster with filter sizes > half of image sizes.
Disadvantage of method 2 of border handling:
Horizontal/vertical border artefacts after extremely flat horizontal and vertical filtering such as Nx1 and 1xN filter sizes → Experiments of Averaging Real Images.
Border handling is more complicated with color images. In order to avoid to write the code three times, its better to transfer first the three A2 arrays into one WriteableBitmap object where all colors of a pixel are unified in one integer and to handle the borders within the WriteableBitmap object.
The following example isn't realistic: The input image is just 11x10 and the 5x5 filter destroys it completely.
It just demonstrates the effect of border handling following method 2.
Please notice:
1. The brightest filter pixel is on the original's neck.
2. Border stripes of thickness 2 look like being 3 pixels thick.
3. A homogenous 3x3 block appears in each of the 4 edges.
Averaging Real Images
Problem 1: Huge memory size is needed.
Sample: Filtering a 6 mio pixel color image of 3000x2000 requires roughly 300 MB fast memory space:
1.1 Stream which loads the input image from hard disk or from network = 6 mio integers = 24 MB
1.2 Image object for displaying the input on the screen = 6 mio integers = 24 MB
1.3 A WritableBitmap that allows to read integer pixels = 6 mio integers = 24 MB
1.4 Three byte arrays R0, G0, B0 containing the red, green, blue values = 3 * 6 mio bytes = 18 MB
1.6 Three integer arrays R1, G1, B1 for intermediary storage = 3 * 6 mio integers = 72 MB
1.7 Three integer arrays R2, G2, B2 to store the output = 3 * 6 mio integers = 72 MB
1.8 A WritableBitmap that allows to store the three colors of a pixel inside one integer = 6 mio integers = 24 MB
1.9 Image object for displaying the output on the screen = 6 mio integers = 24 MB
Problem 2: Filtering is time consuming.
Sample: The simple 11x11 average filter requires 3000*2000*11*11 additions and 3000*2000 divisions and roundings.
Filtering big images with big kernels can take up to 1000 seconds.
Consequences:
The filter algorithm must run in a
background thread in order not to block the complete computer and its user interface for a long time.
The user must obtain a visual information that filtering is still running ( hourglass mouse pointer or progress bar or explicit warning of the expected filter time ) otherwise he/she supects a computer crash and panics instead of waiting.
Many people believe that C# running in the Silverlight browser plugin should be slow.
This is not the case. The same C#-filter running in a local exe takes the same time.
But the difference is, that the Silverlight browser plugin doesn't run unsafe code for sake of security but a local C#-exe does (the user will be warned at start).
Pointers are allowed inside a C#-exe within an unsafe {....} clause and good pointer programmig shortens the filter execution time at least to half.
Further acceleration is possible by writing the filter in native C++. Optimized C++ filters can be found in Intel's image processing library IPP for 200$.
***************************************************************************
Experiments:
***************************************************************************
Choose filter size 25x25.
Switch between Simple Filter and Fast Filter.
Compare the results and the execution times.
***************************************************************************
Choose flat filters size such as 1x25, 1x101, 1x201.
Choose flat filters size such as 25x1, 101x1, 201x1.
***************************************************************************
Choose 1x1 filtering.
Switch between Simple Filter and Fast Filter.
Compare the execution times.
***************************************************************************
Choose Maximum x Maximum filtering.
Switch between Simple Filter and Fast Filter.
Both filters need nearly the same time, because there is just one output pixel an the rest is border handling.
***************************************************************************
Open a bigger JPG or PNG image.
Try out and notice execution times compared to the smaller image using the same filter size.
***************************************************************************
Choose an extremely flat filter size such as 60x1.
Horizontal/vertical strips occur at the right border → disadvantage of border handling method 2.
***************************************************************************
|
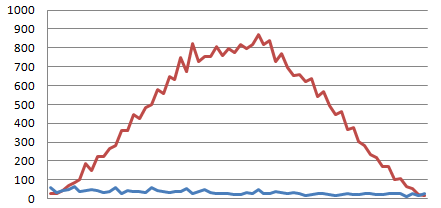
Comparison of execution time of the simple average filter (red) and of the fast average filter (blue):
A 128x128 color PNG test image was filtered with all possible quadratic 1x1, 3x3, 5x5, ... ,127x127 kernels using the above Silverlight program (Firefox-plugin) on a tiny sub-notebook.
The horizontal axis indicates the kernel growth from 1x1 (left) to 127x127 (right).
The vertical axis indicates the time consumption in milliseconds.
The measured times don't include image loading, memory allocation and filtered image display
but they include the thread start+complete events and border handling.
Summary:
1. In case of the simple average filter, there is just a linear (no quadratic!) growth of execution time until the kernel size reaches half of the image size and bigger kernels need lesser and lesser time because the borders grow and the no of averaged pixels shrinks.
2. The execution time of the fast filter doesn't dependend on the kernel size. (But of course it depends on the image size!)
3. With tiny kernels up to 5x5, the simple filter is faster than the fast filter.
| |
 |

Questions & Answers
******************************************************************************************************
Q: What is "Noise" ? Where does it come from ?
A: The additional superposition of an ideal image i[y,x] with a 2D-random function r[y,x].
Any real image is composed of: realImage[y,x] = i[y,x] + r[y,x].
Most important physical cause: Stochastic Brownian motion in the camera's sensor array.
******************************************************************************************************
Q: What is a lowpass filter ? Benefit ? Disadvantage ?
A: Artificial defocusing. It reduces noise. It blurs the image → loss of sharpness.
******************************************************************************************************
Q: What is an average filter ?
A: A lowpass filter that computes the average gray or color value inside a rectangular neighborhood = kernel around all pixels.
******************************************************************************************************
Q: Pseudo code of the simple 3x3 average filter ?
A: for any row y
for any column x
{ for any yy=-1 to yy=1
for any xx=-1 to xx=1
sum += imageIn[y+yy,x+xx];
imageOut[y,x] = sum / 9;
}
******************************************************************************************************
Q: Pseudo code of the simple 9x9 average filter ?
A: for any row y
for any column x
{ for any yy=-4 to yy=4
for any xx=-4 to xx=4
sum += imageIn[y+yy,x+xx];
imageOut[y,x] = sum / 81;
}
******************************************************************************************************
Q: Pseudo code of the 5x5 fast average filter of an input image A0[ySize,xSize] ?
A: Clear the intermediary array A1 and the output A2 but not the input A0
for any column 2 to xSize-3
fill A1 with the sums of 5 horizontaly adjacent A0
for any row 2 to ySize-3
fill A2 with the sums of 5 verticaly adjacent A1
Divide any value inside A2 by 25 and round it
******************************************************************************************************
Q: Why do most filters have uneven kernel sizes such as 3x3, 5x5, 7x7 etc. ?
A: Because of symmetry of the neighborhood above, below, left and right of pixel[y,x].
******************************************************************************************************
Q: What is the "border problem" of any n*n filter ?
A: The n/2 border rows and columns at top, bottom, left and right of the filter image remain unfiltered.
******************************************************************************************************
Q: Pseudo code of the 5x5 "border handling by copy" of a filtered output image[ySize,xSize] ?
A: Fill the uppermost 2 rows with the content of the 3. row.
Fill the lowermost 2 rows with the content of the ySize-3 row.
Fill the leftmost 2 columns with the content of the 3. column.
Fill the rightmost 2 columns with the content of the xSize-3 column.
******************************************************************************************************
Q: Why do we address 2D-arrays such as pixel[height,width] with y at first followed by x
and why do the double for-loops start with looping y ?
A: We want to read and write 2D-arrays row by row from left to right.
The other way we would read them column by column from top to bottom.
*******************************************************************************************************
*******************************************************************************************************
Further readings: www.kovalevsky.de/ImProc/L01_Noise/Noise_e.htm




