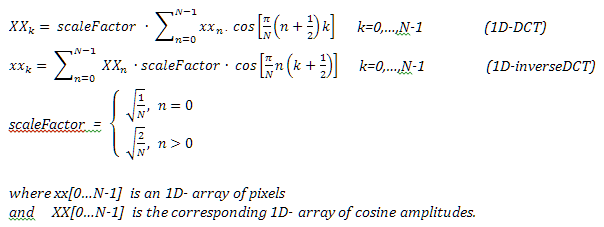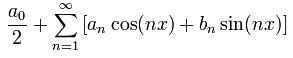|
Image Processing 1: Filters
1.6 The Discrete Cosine Transform Filter
1.6.1 Sample of a 1D Discrete Cosine Transform and of its Back Transform
1.6.2 Sample of a 1D Discrete Cosine Transform with a Limited Back Transform
1.6.3 2D Discrete Cosine Transform of monochrome images
1.6.4 2D Discrete Cosine Transform of color images
1.6.5 Questions & Answers
Copyright © by V. Miszalok, last update: 2011-09-22 |

Let me know
what you think
|
The Discrete Cosine Transform DCT
The Discrete Cosine Transform DCT is derivated from the Discrete Fourier Transform DFT.
It maps an array of equidistant spatial or time values xx[0...N-1] into the frequency domain,
that is to say into
amplitudes XX[0...N-1] of N cosine basis functions.
The inverse DCT (synonym: DCT back transform) can exactly restore xx from XX but in most cases
varied filtering is applied by restricting the back transform to a limited set of frequencies.
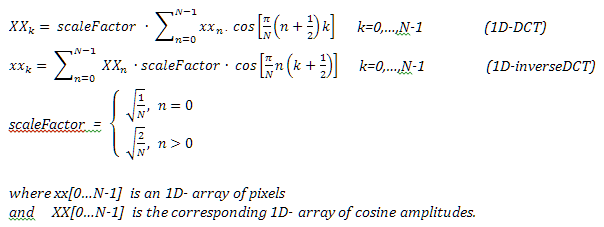
See Wikipedia: DCT
and DFT
and Miszalok: Lecture on the Fourier Transform
//C#-Code of the Discrete Cosine Transform DCT and of its back transform:
//xx[0...N-1] = spatial domain input/output array, XX[0...N-1] = frequency domain array
private void DCT( float[] xx, float[] XX )
{ int k, n, N = xx.Length;
float sum;
float scaleFactor0 = (float)Math.Sqrt( 1.0 / N );
float scaleFactor = (float)Math.Sqrt( 2.0 / N );
double piN = Math.PI / N;
for ( k=0; k < N; k++ )
{ sum = 0;
for ( n=0; n < N; n++ ) sum += xx[n] * (float)Math.Cos( piN*(n+0.5)*k );
if ( k==0 ) XX[k] = sum * scaleFactor0;
else XX[k] = sum * scaleFactor ;
}
}
private void DCTBack( float[] XX, float[] xx )
{ int k, n;
float sum;
float scaleFactor0 = (float)Math.Sqrt( 1.0 / N );
float scaleFactor = (float)Math.Sqrt( 2.0 / N );
double piN = Math.PI / N;
for ( k = 0; k < N; k++ )
{ sum = XX[0] * scaleFactor0;
for ( n = 1; n < N; n++ ) sum += XX[n] * scaleFactor * (float)Math.Cos( piN*n*(k+0.5) );
xx[k] = sum;
}
}
Sample of a 1D Discrete Cosine Transform and of its Back Transform
Drag the sliders to generate input !
It is easy to install, run and zoom this sample program out of the browser:
Right click the sample → Install DCT1D Application onto this computer... →
Uncheck Start menu, check Desktop → OK → Click the DCT1D Application icon.
To uninstall DCT1D from your computer, just right click the running application → Remove this application... → Yes.
******************************************************************************************************
Experiments:
1. Drag the sliders arbitrarily.
2. Drag all sliders to 0.
3. Drag all sliders to 100.
4. Drag 1., 3., 5., etc. sliders to 0 and 2., 4., 6., etc. sliders to 100. Result: frequencies 2, 4, 6, 8, 10 are almost 0.
5. Drag 1+2, 5+6, 9+10 to 100 and all others to 0. Result: frequencies 2, 4, 6, 8, 10 are almost 0.
******************************************************************************************************
Sample of a 1D Discrete Cosine Transform with a Limited Back Transform
Drag the sliders to generate input and select frequencies !
To run this program out of the browser, see the guidance above underneath the first sample program.
//Just one line changed within the Discrete Cosine Transform back transform.
//xx[0...N-1] = spatial domain input/output array, XX[0...N-1] = frequency domain array
private void DCTBack( float[] XX, float[] xx )
{ int k, n;
float sum;
float scaleFactor0 = (float)Math.Sqrt( 1.0 / N );
float scaleFactor = (float)Math.Sqrt( 2.0 / N );
double piN = Math.PI / N;
for ( k = 0; k < N; k++ )
{ sum = XX[0] * scaleFactor0;
for ( n = 1; n < N; n++ )
if ( cb[n].IsChecked == true ) sum += XX[n] * scaleFactor * (float)Math.Cos( piN*n*(k+0.5) );
xx[k] = sum;
}
}
******************************************************************************************************
Experiments:
1. Drag the sliders arbitrarily.
2. Drag all sliders to 0.
3. Drag all sliders to 100.
4. Drag 1., 3., 5., etc. sliders to 0 and 2., 4., 6., etc. sliders to 100.
******************************************************************************************************
2D Discrete Cosine Transform of monochrome images
The algorithm needs 6 big arrays:
img0 = new WriteableBitmap(BitmapImage); //original JPG or PNG image
Byte [,] R0 = new Byte [ySize,xSize] //red channel values from img0
float[,] R1 = new float[ySize,xSize] //horizontally transformed R0
float[,] R2 = new float[ySize,xSize] //vertically transformed R1
float[,] R3 = new float[ySize,xSize] //vertically back transformed R2
img1 = new WriteableBitmap(xSize,ySize); //horizontally back transformed R3
| | The 2D DCT consist of two consecutive 1D-DCTs and its 2D back transform consists of 2 consecutive 1D-inverseDCTs. |
| 1. | horizontal 1D-DCT of all rows of R0 to R1. |
| 2. | vertical 1D-DCT of all columns of R1 to R2.
R2 is the 2D-DCT matrix. |
| 3. | vertical 1D-inverseDCT of all columns of R2 to R3 restricted to frequencies between VerticLowest and VerticHighest. |
| 4. | horizontal 1D-inverseDCT of all rows of R3 to img1 restricted to frequencies between HorizLowest and HorizHighest. |
To run this program out of the browser, see the guidance above underneath the first sample program.
******************************************************************************************************
Experiments:
For small slider increments and decrements click first on the horizontal guide rail right or left and finally click the valve itself.
1. Lower HorizHighestFrequ down to 3.
2. Lower VerticHighestFrequ down to 3..
3. Increase HorizLowestFrequ to 4, 5, 6 .....
4. Increase VerticLowestFrequ to 4, 5, 6 ....
5. Shift all sliders to their minimum and increment both HighestFrequ-Sliders stepwise to 4, 5, 6 etc.
6. a) Shift VerticLowestFrequ to 1 and VerticHighestFrequ to maximum.
b) Shift both horizontal frequencies to minimum.
c) Increment HorizLowestFrequ to 2, 3, 4, etc.
d) HorizHighestFrequ automatically increments to 5, 6, 7 etc.
e) The narrow horizontal bandwidth results in strange artefacts.
7. a) Shift HorizLowestFrequ to 1 and HorizHighestFrequ to maximum.
b) Try the same as 6. b), c), d) e) in vertical direction.
******************************************************************************************************
2D Discrete Cosine Transform of color images
To run this program out of the browser, see the guidance above underneath the first sample program.
******************************************************************************************************
Experiments: Same as for monochrome images above.
******************************************************************************************************
Questions & Answers
******************************************************************************************************
Q: What is the Fourier series ?
| A: | A function F(x) is represented as the sum of sine- and cosine-waves: |
| F(x) = | 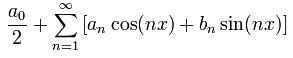 |
******************************************************************************************************
Q: What is the cosine series ? Comparison to Fourier series ?
A: Fourier: Base functions: cosine and sine.
Cosine: Base functions: just cosine.
Advantage of cosine: No complex additions and multiplications necessary → less complicated algorithm
Both need nearly the same considerable computational time.
******************************************************************************************************
Q: What sorts of image filters are possible using the inverseDFT or the inverseDCT ?
Advantages, disadvantages compared with other filters ?
A;
1. Lowpass filtering by leaving out high frequencies
2. Highpass filtering by leaving out low frequencies
3. Bandpass filtering by leaving out low and high frequencies
Advantages:
1. Easy filtering of images that are derived from frequency measurements ( CT, NMR, Radar, Sonar etc ).
2. Easy removing of known interference frequencies.
3. Intergrated circuits specialized on DCT are available.
4. Well suited for lossy image compression
Disadvatages:
1. Extensive computation time whithout specialized hardware.
2. Leaving out important frequencies can produce severe artefacts.
******************************************************************************************************
Q: Computing time of DFT and DCT of an NxN image ? What is FFT ?
Both DFT and DCT and their inverse transforms run 3 nested for-loops 0...N
which results in N3 operations.
The Fast Fourier Transform FFT reduces N3 to log2N*N2 operations.
Drawback: The FFT assumes N being a power of 2 as 128, 256, 512 etc.
******************************************************************************************************
Q: JPG is a lossy image compression standard basing on DCT. Why is it so fast ?
A: The image is subdivided into small 8x8 pixel blocks which undergo DCT.
The resulting data for all 8x8 blocks is further compressed by Huffmann encoding.
Nowadays all modern graphic chips contain a processor pipeline specialized in DCT and Huffmann encoding.